
|
got a virus? |

|
|---|
|
|
PC Technician computer tips and help

If you want to follow my exploits as a pc technician - click on button.
It can be very rewarding to solve computer problems but there are times
when a sledge hammer would be the appropriate tool of choice.
|
How to build a computer
See the video below on how to build a computer. This is part 1 of a three part series. In total the videos run about 2 hours. If you have some skills in building things then you may want to try this - but be warned - a lot of people I know tried to do this but invariably come to me to complete the job. It can be a rewarding experience to actually build one, not to mention the fun that goes along with the process. |
This is part 2 in the series - the actual assembly of the components. This is part 3 in the series - installing windows and additional tweaks. |
 |
|
| THE GEEK SIDE |

|
Shop Amazon - Contract Cell Phones & Service Plans |
|
|
Buffon Needle Problem - Computer Simulation
One can calculate the value of π by dropping a needle of length k onto a grid of parallel lines whose length is greater than k. The value is determined as the probability of hits (the needle crosses a grid line) to the total number of tosses. This value is π = ( 2 * k * total-tosses) / (number-of-hits). This calculation was simulated with a computer program. The program was run on several platforms and processors. I ran the simulation for 10 million tosses and a needle length of .8. I assumed the grid lines to be one unit apart. ...see results.... |
|
Simulation - Normal Distribution Watch the balls drop - produces bell-shaped curve Click on image to stop - when bored click here for more on simulations. |
|
Math can be fun Can 1919 be represented as the sum of a cube and a fourth power? ANS: Click on bookworm for answer and more |

|
| As I was trying to solve this problem, I started to think tangentially about how would I be able to get the last five digits using a computer program written in basic. Using double precision , ie, 64 bits to get the result would not do it. Since only 52 bits are involved in expressing the "precision". The other 11 bits are used for the exponent. Well, 252 can only give a precision to 16 places - not enough. Using double precision interger arithmetic does not do it either - only 10 places. So I investigated the ways to do high precision numerical calculations. I stumbled across this ARTICLE. Yikes! More than I could handle. So, just for laughs I tried the windows calculator and lo and behold and dipped in butter fat, I got the full answer - try it. Also try to do 2128 to see the number of places that can be expressed ( the upper limit - about 32 places) Obviously, a high precision alogrithm is used in the calculator - and this is how I get my kicks. By the way the breakoff point ( where the result is displayed as an exponent ) is somewhere between 2 106 and 2 107. Quick son - get the Prozac. |
|
Fun with Biology I never really got to study biology. As a boy I started out with chemistry and my fascination lead to all kinds of dangerous experiments. In those early days, you could walk into a chemical supply house and buy really dangerous stuff. The only exception was concentrated acids. It was a good thing I couldn't get those acids as I wanted to make guncotton - probably saved my life. My interests then shifted to physics and mathematics and then one day I read a book by Erwin Schrödinger - called "What is life". Schrödinger is the physicist who developed the equation that describes quantum mechanical behavior. In the book, he ponders the question of what is life and in an apologetic manner ( since he is a physicist and not a biologist ) questions how a virus can actually express the attributes of a living system. Since a virus is composed of approximately several hundred thousand molecules, then how is it that the virus can behave the way it does. The relatively small number of molecules cannot act, statistically speaking, the same way as a living cell like a human cell which has about 10 trillion molecules. Schrödinger then made the case that a virus must do what it does by playing by the rules of quantum mechanics. I then got lost in his analysis and decided to view biology on a more rudimentary level and to just enjoy the wonderful and strange facts from biology which can be found HERE . |
>
|
Fun with your Photographs |
| I found two programs that manipulate photographs to give some interesting results. One program is actually an online web site where you can upload a photo ( of yourself ) and turn it into a cartoon image. You can upload the photo from your computer or from a url. Once uploaded - the program "cartoonizes" the photo and in about 30 seconds - it is displayed for you to download. The result looks great and a second benefit is that it is absolutely free. You can try it yourself HERE. The second program is a free download. This program called "FotoSketcher" will take an image and turn it into a painting. The program has a nice user interface and a lot of assorted effects to transform your photo. For example, it can produce sketches in oil or pastel, pen and ink, oil painting with several types of painting effects, and some other stylized effects. I liked this program so much I sent the author some coffee money - (as he put it ) as a donation. Well, I sent him enough money to buy a couple of Starbucks coffees. You can get the program HERE. |
>
|
If you need a computer or computer related
supplies - or just about anything else - then
use the amazon search box below. You can purchase new or used items - to save a few bucks. |
>

|
|
Free Wallpaper
We have some photos that you can use as wallpaper. Just click on a link below - when image is shown - right click on the image and click on "Set as Background". This image should now be your desktop background. |
|
· Hawaiian beach
· Hawaiian Cliffs · Country scene · Fireworks · Fountain · Halloween · Moon · Country road · Shield · Hawaiian stream · Country stream · Grand Canyon · Grand Canyon Window · Bryce Canyon |
|---|
>
 Need to chill out?
Need to chill out? Then click on surfer. |
|---|
| Some facts + LSNED (Learn Something New Every Day) |
| Archive-LSNED |
| Strange Biology Facts |
| Terrific Fractal Art |
>
>
| Fun with Physics | |
|
In case you missed it - the world of physics is on the threshold of important
particle physics discoveries. In Geneva, Switzerland a particle accelerator
called the Large Hadron Collider (LHC) is now operating at about half of
its full power. The LHC collides beams of protons together to "see" the
constituents of protons. It is hoped that these experiments will provide
some answers to the fundamental nature of matter. One such quest is
to determine the existence of the Higgs boson. The so-called god particle
which according to theory - gives mass to the known particles. So the
Higgs particle and its associated field gives mass to all particles which
includes the proton - the building block of matter. The theory of particles
is called QCD ( Quantum Chromodynamics ) and recently, physicists have
used this theory with some approximations to create a computational
framework in which to calculate the mass of the proton. So, from
first principles a basic constant of nature , ie, the mass of the proton
was calculated using supercomputers. These computations would
not be possible without the computer. So, by performing an enormous
number of calculations the mass was determined. You have to understand
the components of a proton ( quarks, which have a mass total less than
the proton and gluons, which are massless) cannot just be added up
to get the mass of the proton. In fact, these calculations say that even if
the quark masses vanished, the proton mass would not change much.
Now that's computing. The interior of a proton is a bee-hive of activity
with the gluons and quarks interacting like crazy and for computers
to unravel this mess - is truly amazing. To summarize, using QCD and
assuming zero mass for the quarks, and zero mass for the gluons, and
that space is not continuous but a grid like structure and allowing
the grid points to approach zero and of course a supercomputer -
the mass of the proton was calculated to within 10% of its measured value!
Now put that in your pipe - Einstein (who by the way did not accept quantum mechanics or at least thought that it was an incomplete theory) See a pictorial representation of the interior of a hadron (image below). If you aren't bored out of your mind yet - then see more on particle physics HERE. |
|
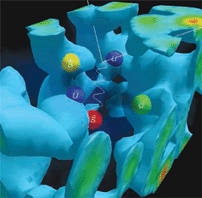 The interior of a hadron, such as the proton or neutron, is not static. Gluons fluctuate in a collective
fashion, illustrated by the red-orange-yellow-green-blue fluid. Sometimes the gluon field produces extra
quark-antiquark pairs; here, a proton (uud) has fluctuated into a ? hyperon (uds) and a kaon (u).
CREDIT: D. LEINWEBER/CENTRE FOR THE SUBATOMIC STRUCTURE OF MATTER, UNIVERSITY OF
ADELAIDE
The interior of a hadron, such as the proton or neutron, is not static. Gluons fluctuate in a collective
fashion, illustrated by the red-orange-yellow-green-blue fluid. Sometimes the gluon field produces extra
quark-antiquark pairs; here, a proton (uud) has fluctuated into a ? hyperon (uds) and a kaon (u).
CREDIT: D. LEINWEBER/CENTRE FOR THE SUBATOMIC STRUCTURE OF MATTER, UNIVERSITY OF
ADELAIDE
|
>
| Fun with Probability |
|
It is not always easy to grasp the concepts and implications
of probabilty theory. For example, a problem in probability
called the "Monty Hall" problem illustratates some of the
difficulty. The problem goes like this:
Based on the the old TV show "let's make a deal" hosted by Monty Hall - there are three doors , two of which contain a zonk and one contains a prize. The contestant is asked to choose a door. Then Monty reveals what's behind one of the other doors ( he shows the one containing the zonk). So with one door revealed ( a zonk) that leaves two closed doors - the one picked by the contestant and the other door. Now Monty asks the contestant - "do you want to switch the door you picked with the other closed door?" Well, what is the best strategy for the contestant? Initially, it looks like it shouldn't make a difference - that is, with only two doors left it would appear the contestant would have a fifty-fifty chance of being correct. Well, wrong!! His best strategy would be to switch doors to win the prize. And why is that? Well, it all boils down to a change in information. At first, there were three doors and the chance of picking the prize is 1/3 but it also means that the chance of being wrong is 2/3. So 2/3 's of the time he will be wrong - thus with this new information, ie, he has a door that has a 2/3 chance of being wrong, then the best strategy would be to switch doors. |
| Not Convinced - Try it a few hundered thousand times |
|
Enter the number of trials and the number of doors and click
run to see the effect of switching or not switching doors.
The simulation run by this window randomly selects which door
wins and randomly selects the player's ( Alice or Bob )
initial choice. Monty Hall then opens one of the remaining
doors which is a loser. Then Alice always stays
with her original door and Bob always switches.
|
>
| Fun with Cryptology |
|
What is cryptology? First of all cryptology is the science
of cryptography ( codemaking) and cryptanalysis (codebreaking).
We will examine cryptography and try to understand how it
works, since we see it all the time when we send an encrypted
message. To a cryptologist, codes and ciphers are two
different concepts. Codes refer to substitutions for letters,
words, or phrases and a cipher is an algorithm to transform
a message into a meaningless jumble. Most of these algorithms
use the concept of a key - which is used in the algorithm to
produce the jumbled message. For example, if we want to
send a message that says "attack" that is encrypted, we could
assign a number to each letter - ie, a=1, t=20, c=3, and k=11.
Thus the message could be sent as 1 20 20 1 3 11 Well, this is not very secure as it is easy to figure out with very little effort, what the message is. So, the next step would be to use a key to further encrypt this message. Okay so let's pick a key that is equal to 5. Now the message becomes: 5 100 100 5 15 55 which also is not secure as it obvious the numbers are all divisible by the same number ie, 5. Now what do we have to do - to send a secure message. We would need a not so obvious key to encipher the message and another key to decipher the message. Fortunately, there is such a method. It is called public key encryption. There are two components to pubic key encryption - a public key and a private key. The public key is used to encrypt ( encipher ) the message and the private key is used to decrypt ( decipher) the message. The public key is available to anyone who wants to send an encrypted message but we want the private key to be known only be the recipient of the message. We obviously don't want to send the private key along with the message, as it may be intercepted and used to decipher the message. The problem is, how do we reduce the exposure of the private key to zero. This is not a simple problem but some very clever people came up with the solution, it is called RSA encryption. Named after the people who invented it ( Rivest, Shamir, and Adleman). How does this work? Let's assume Mary wants Bill to send her a secret message. She would need to generate two keys - public and private. She puts the public key on her website for anybody to read. Bill uses this public key to encipher his message and sends it to Mary. She uses her private key to decipher the message. This was all done without having to send a private key along with the message. So this is secure as long as the public and private keys are not breakable. To ensure this to be the case - the algorithm incorporates a method using 2 really big prime numbers to generate both keys. In fact, it is the product of the 2 big prime numbers that is actually used, the product in fact is a really huge number. This huge number is actually used to generate the keys and it's unbreakability is based on the fact that it is extremely difficult to take a huge number and find the two prime factors that make it up. For example, the largest number yet factored is 155 digits long and it took about 300 computers ( fast workstations) more than seven months to get the two prime factors. Well, this all sounds good but what about the details - show me an example of the algorithm to encrypt and decrypt a message. Okay, if you think you have seen enough you can skip the gory details otherwise you can go HERE to see the inner workings of the algorithm. |
>
>
>

|
Everyone is familiar with big AL's formula equating energy and mass - but where did it come from? Einstein's dervivation is a bit tricky to grasp - but here is a derivation he perfomed later that really only used simple principles and mathematics. Check it out HERE. |
>
>





